Detecting Fraudulent Transactions

Low banking penetration is prevalent in many parts of Sub-Saharan Africa (SSA). This is partially driven by low trust towards banking institutions for historical reasons, low and often intermittent income, lack of identity documentation and in certain cases a general lack of physical banking infrastructure in remote, rural areas where a large chunk of populations often stay in some parts of SSA.

In light of these issues, numerous fintechs have arisen in an attempt to provide an elixir to these issues, with the end goal of leveraging increasing smartphone penetration and affordability to build the digital economy. This is often seen as a net positive, particularly when it leads to an increase in cashless transactions as it reduces the security concerns of carrying around cash and improves the convenience of transacting which often results in an overall increase in economic activity. In countries where a lot of business occurs informally, this also adds more transparency by creating an audit trail of transactions minimising tax evasion.

In Zimbabwe, this created an option for the government to tax informal businesses by taxing every transaction carried out through the dominant mobile money system Ecocash — because a country can fail at everything except collecting tax.

Source: 9gagSetting the scene

We can go on about the benefits, but let us take a step back from the big picture and imagine we are running a payments company in an African country… let’s call the country Wakanda. We facilitate payments between parties. While we are trying to make payments as seamless and convenient as possible we start encountering one of the negative aspects of cashless payments: cyber fraud.

To flag these transactions we decide to build a model that can predict whether a given transaction is fraudulent or not. In light of this scenario, I decided to look at the Credit Card Fraud Detection dataset on Kaggle with the intention of using machine learning to determine whether or not a given transaction is fraudulent or not.

Dealing with the dataset

I decided to start off with a visualisation of both normal and fraudulent transactions. The idea behind this is to get a better understanding of what the data actually looks like.

#loading the datasetlocation = '/Users/emmanuels/Downloads/creditcard.csv'dat = pd.read_csv(location)

#visualising transactionsax = dat.groupby('Class').size().transform(lambda x: (x/sum(x)*100)).plot.bar()for a in ax.patches:    ax.text(a.get_x()+.06,a.get_height()+.5,\           str('{}%'.format(round(a.get_height(),3))),fontsize=24,              color='black')old = [0,1]new = ['Normal','Fraudulent']ax.set_xticks(old)ax.set_xticklabels(new,rotation=0,fontsize=28)

After loading the data, I grouped my dataset by class (with 0 representing a normal transaction and 1 a fraudulent one), returning the total count of each class. While the apply operation would allow me to literally apply any lambda function to my grouped dataset, in this context, using the transform returns results that are the same size as what I inputted. This is then converted to a percentage of the total number of transactions in my lambda function and then plotted to a bar-plot and annotated with the relevant percentages.

Percentage of normal and fraudulent transactions

As expected, we see that a significant proportion of transactions are non-fraudulent. This presents a small problem; if I want to measure the performance of the machine learning models I use, I cannot rely purely on the accuracy score. If for example, I were to predict that every single transaction was not fraudulent I would achieve an accuracy score of 99.827%. This sounds great, however, I would have failed to classify a single fraudulent transaction resulting in a loss of revenue due to fraud. Whatever metric I use to measure the performance of my algorithm, I may need to place greater importance on the model’s ability to correctly classify fraudulent transactions.

Visualising Volume of transactions by time

As a next step, I wanted to understand the volume of transactions according to the time the transaction was made. Since the dataset is anonymised from the time perspective I only have the number of seconds the transactions were made after the first recorded transaction.

plt.plot( 'Time', 'Amount', data=dat, marker='o', color='blue',                  linewidth=2, linestyle='dashed')plt.xlabel('Seconds since first transaction')plt.ylabel('Size of transaction')plt.rcParams["figure.figsize"] = (30,20)plt.rcParams["font.size"] = "20"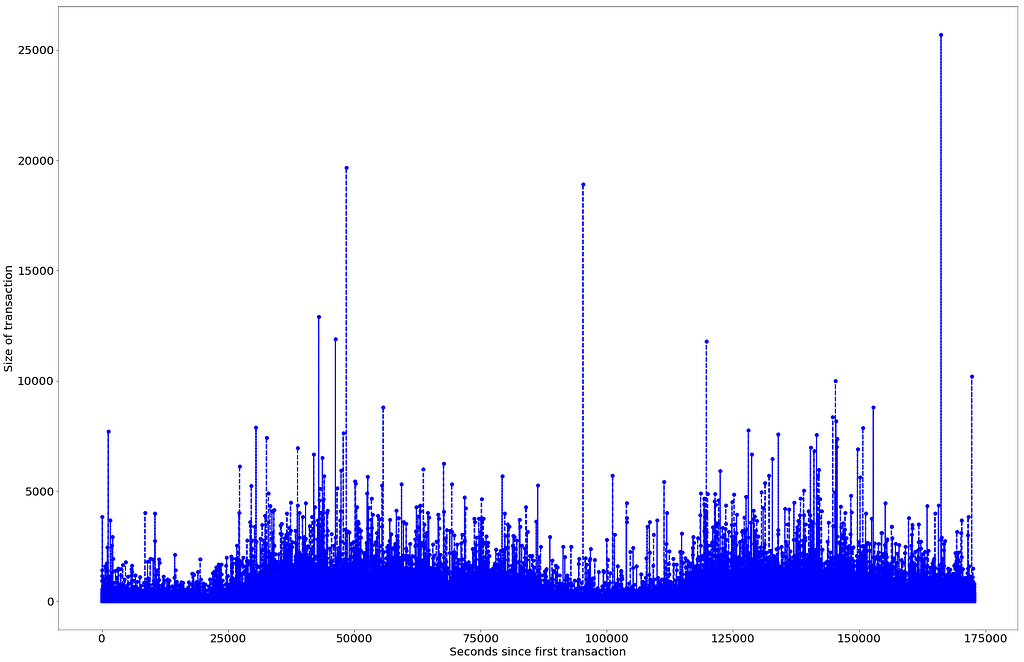

Volume of transactions over time

Plotting the volume of transactions over time seems to show a bit of a pattern. The volume increases at around the 25000 seconds mark, peaking 20000 seconds later and then steadily declining. This cycle seems to last for around 50 000 seconds or close to 14 hours. The same pattern emerges again at the 125 000 mark. This could presumably be the daily cycle, transactions start increasing during the start of the day, peaking sometime in the middle of the cycle and declining before close of business. Presumably, this pattern could reveal something about when fraudulent transactions are more likely to occur.

dat['Hours'] = dat['Time']/3600

To include this in my analysis I created a column that would indicate the hour in which a transaction occurred. To repeat, the assumption is that this could potentially be a useful feature in correctly indicating whether a transaction is normal or fraudulent.

Visualising proportion of fraudulent transactions over time

Following the assumption I made in the previous paragraph, I decided to visualise the percentage of fraudulent transactions over the course of time just to find out if fraudulent transactions tend to be clustered around a particular time range.

#visualising amount spent per hour by classdat_grouped = dat.groupby(['Hours','Class'])['Amount'].sum()ax_three = dat_grouped.groupby(level=0).apply(lambda x:round(100*x/x.sum(),3)).unstack().plot.bar(stacked=True)for i in ax_three.patches:    width,height=i.get_width(),i.get_height()    x,y = i.get_xy()    horiz_offset=1    vert_offset=1    labels = ['Normal','Fraudulent']    ax_three.legend(bbox_to_anchor=(horiz_offset,vert_offset),labels=labels)    if height > 0:        ax_three.annotate('{:.2f} %'.format(height),                         (i.get_x()+.15*width,                         i.get_y()+.5*height),        rotation=90)

To create this visualisation I grouped my dataset by both hours and class, returning the sum of transactions that occurred in each hour that were either normal or fraudulent transactions. I then applied a lambda function that would convert the amounts for both classes to percentages, created a stacked bar-plot and annotated it with the relevant percentages, positioning the percentages to ensure that the plot is readable.

Data Viz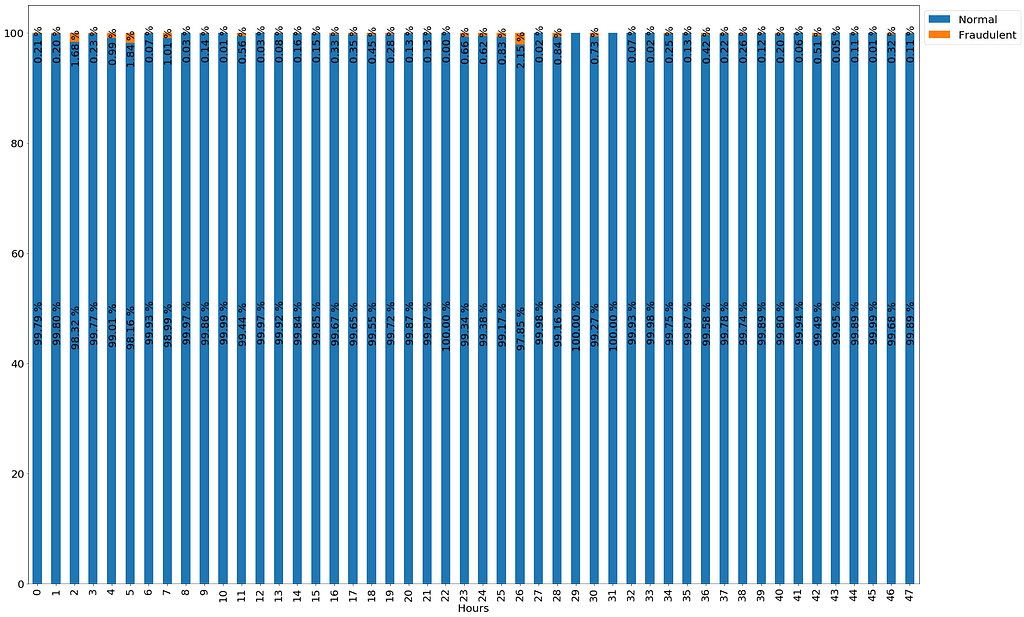Percentage of fraudulent transaction over time

Since the data is only dealing with transactions within a 48-hour time frame, any observable patterns could be explained away by chance. However, I thought it would be interesting to add the percentage of fraudulent transactions that occurred within the hour in which a particular transaction was carried out as a feature. The assumption I have is that it is possible that the hour in which a transaction was carried out could contain information that could help me classify (along with other features) whether a transaction is fraudulent or not. I think it might be conceivable that fraudulent transactions would be more prevalent during certain hours of the day.

a= dat.groupby(['Hours','Class'])['Amount'].sum()b =pd.DataFrame(a.groupby(level=0).apply(lambda x:round(100*x/x.sum(),3)).unstack())b=b.reset_index()b.columns = ['Hours','Normal','Fraudulent']dat = pd.merge(dat,b[['Hours','Fraudulent']],on='Hours', how='inner')

In order to create this column, I started off by calculating the percentage of both fraudulent and normal transactions by hour, and unstacked the results in order to return the classes as columns.

I then merged the dataframes, taking only the fraudulent column from the dataframe I had just created. Like in SQL, I merged the two dataframes on two common traits/keys — hours. After this, my dataframe had a new column showing the percentage of fraudulent transactions that occurred in the hour in which a given transaction was carried out.

The machine learning begins

To start off the classification process, I decided to start off with logistic regression. In one of my previous articles, I gave a short explanation of this regression algorithm. To recap, the logit function carries out a transformation that returns the probability of an event occurring.

Statistics = Machine Learning

dat.columns[df.isnull().any()]dat['Fraudulent'] = dat['Fraudulent'].fillna(0)from sklearn.linear_model import LogisticRegressionfrom sklearn.model_selection import train_test_split#from sklearn.feature_selection import RFEfrom sklearn.metrics import confusion_matrixfrom sklearn.metrics import classification_reportlog_reg = LogisticRegression(penalty='l1')y = dat['Class']X = dat.drop(['Class'],axis=1)X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=100)log_reg.fit(X_train,y_train)#predicting with modelspredicts = log_reg.predict(X_test)#f1 score is harmonic mean of recall and precision scoreconfusion_matrix(y_test,predicts)

####RESULTS####array([[85276,    25],       [   46,    96]])

I proceeded to check for NAN values and replaced all NANs with 0 where relevant. After this cleanup process I imported the packages I would need for my analysis, split my data into training and test data and fit the logistic regression model to my training data. For this model, I specifically used l1 regularisation (lasso regression- Least Absolute Shrinkage and Selection Operator). while l2 minimises the sum of squares, l1 minimises the sum of the absolute differences between the target and estimated values. This regularisation process is carried out to prevent the coefficients from overfitting, potentially increasing my model’s ability to generalise to new data.

As discussed in an earlier paragraph, the accuracy score would not be a good metric to measure how well my model performs, I instead first chose to look at the confusion matrix to see how well my model correctly classifies both normal and fraudulent transactions- paying special attention to my model’s ability to correctly classify fraudulent transactions.

According to the confusion matrix my model correctly classifies normal transactions with 99.974% accuracy, and 67.60% accuracy for fraudulent transactions.

print(classification_report(y_test,predicts))

####RESULTS####              precision    recall  f1-score   support           0       1.00      1.00      1.00     85301           1       0.79      0.68      0.73       142   micro avg       1.00      1.00      1.00     85443   macro avg       0.90      0.84      0.86     85443weighted avg       1.00      1.00      1.00     85443

For ease of comparing models, I printed out the classification report for my predictions. Important for the purposes of consistent comparison, the report returns the f1-score. This the harmonic mean of both the precision (proportion of true positives on all positive predictions)and recall score (proportions of true positives on all actual positive items), the f1_score is kind of a weighted score that shows me how well the model correctly classifies both normal and fraudulent transactions. To determine model performance I am specifically looking to increase the f1_score for class 1 (fraudulent transactions) which would then be reflected by the macro average f1_score.

Recursive Feature Elimination

Not all features are equally important. Some features do not add value to my model’s performance and may even have an adverse effect on performance. Of course, this is highly dependent on the model I am using. Certain models such as decision trees and random forest select the most relevant features without a need for feature selection.

The idea behind feature selection is to select features that optimise a particular score. This can either be done through forward selection (starting with one feature and adding more until we find the combination with the highest score) and backward selection (the inverse of forward selection). For this analysis, I opted to use recursive feature elimination. This is a form of backward selection that drops the features that have the least importance in my model. The importance is dependant on the scoring I am using (how I am measuring importance.

from sklearn.feature_selection import RFECVselector = RFECV(log_reg,step=3,cv=5,scoring='f1_macro')selector = selector.fit(X,y)

I specifically opted to use the recursive feature elimination with cross-validation, this means that the optimal numbers of features will be selected with 5 fold cross-validation (I gave a high-level explanation of the concept of cross-validation in one of my previous blogs). For the scoring, I opted to use the f1_macro score. This is the mean of the f1_score for normal and fraudulent transactions. With the step set at 3, I specified that 3 features should be removed at each iteration.

#showing the name of the features that have been selectedcols = list(X.columns)temp =pd.Series(selector.support_,index=cols)selected_features = temp[temp==True].indexselected_features

#### RESULTS ####Index(['V1', 'V3', 'V4', 'V5', 'V6', 'V7', 'V8', 'V9', 'V10', 'V11', 'V12',       'V13', 'V14', 'V15', 'V16', 'V17', 'V19', 'V20', 'V21', 'V22', 'V23',       'V24', 'V25', 'V27', 'V28', 'Fraudulent'],      dtype='object')

To get a picture of the features returned after running the recursive feature elimination I created a pandas series mapping the features selected to the relevant column titles. This process removed V2, V15, V18, the Hour and Amount and Time column.

X_rfecv = dat[selected_features].valuesX_train,X_test,y_train,y_test = train_test_split(X_rfecv,y,test_size=0.3,random_state=100)log_reg.fit(X_train,y_train)#predicting with modelspredicts = log_reg.predict(X_test)#f1 score is harmonic mean of recall and precision scoreconfusion_matrix(y_test,predicts)

#### RESULTS ####array([[85279,    22],       [   48,    94]])

After fitting the logistic regression model using the features filtered from the rfe process we find a very slight improvement in the model’s ability to predict normal transactions while the inverse applies for fraudulent transactions. The macro f1_score, however, remains the same as it did will all columns factored in as features.

Looking for a better model

I decided to use both a decision tree and random forest with random search cross-validation to get an approximation of the optimal parameters for my classification task and managed to get my macro average f1_score to 0.88 with my random forest. I wrote a brief high-level explanation of both these models in one of my previous blogs.

random_forest = RandomForestClassifier()param_grid = {"criterion":['gini','entropy'],             'n_estimators':range(20,200,20),             'max_depth':range(20,200,20),             }tuned_rfc = RandomizedSearchCV(random_forest,param_grid,cv=5,scoring='f1')tuned_rfc.fit(X_train,y_train)tuned_preds = tuned_rfc.predict(X_test)confusion_matrix(y_test,tuned_preds)

#### RESULTS ####array([[85288,    13],       [   35,   107]])

Using the randomised search package, I preset parameters I wanted to test out to get the optimal parameters for my model. The idea behind this is to find the best combination of parameters from the list of possible parameters. As its name implies, as opposed to testing every possible permutation from the parameters specified, combinations created are random, making it a faster hyper-parameter tuning method than alternatives such as grid search — which would take a much longer time to run making it as fun to run as watching paint dry, or the equivalent… watching a DC movie.

‘DC movies are great’ — no-one

For a deeper understanding of how randomised search works and the mathematics behind it, I have added a link to the original research paper from the Journal of Machine Learning. Using this method and the f1 as the scoring parameter I fitted the optimal parameters and my training data, ran my predictions and returned the confusion matrix. As evidenced in the results, we can see an improvement in both accuracy in predicting normal and fraudulent transactions.

print(classification_report(y_test,tuned_preds))

#### RESULTS ####     precision    recall  f1-score   support           0       1.00      1.00      1.00     85301           1       0.89      0.75      0.82       142   micro avg       1.00      1.00      1.00     85443   macro avg       0.95      0.88      0.91     85443weighted avg       1.00      1.00      1.00     85443

Even more exciting is the increased macro f1 average. I can finally fish out more of those fraudulent transactions.

XGBoost!

As a final step, I decided to try the much-lauded XGBoost Classifier fine-tuned through a cross-validated randomised search. The term XGBoost is actually an abbreviation for extreme gradient boosting. From looking at different Kaggle contests this seemed like a pretty powerful machine learning with great performance. Some say it can even help you predict where you left those individual socks that ‘mysteriously’ go missing after laundry day.

Sock Army Unite!

According to the official ‘white-paper’ XGBoost operates under the gradient boosting framework a gradient tree boosting algorithm (high-level explanation in my previous blog). Put simply, this involves turning a weak learner or tree that does not have a strong ability in predicting our desired outcome into a stronger learner/tree. This means that new trees will be created to correct the residual errors made in the predictions from the previous trees (correcting previous errors). The process continues for as long as we specified, depending on the parameters I am using for my model. You can also control how quickly the model can fit the training dataset by attaching a weighting to the corrections made by each tree that will be added to the model.

From my understanding, XGBoost can be explained best by first looking at how the decision tree works. With decision trees we split our data into subsets or leaves, assigning a score to each leaf and continue building more branches of leaves (splitting up our data more) choosing the leaf with the highest score (information gain) until a pre-defined level/depth is reached. With an ensemble of trees (e.g random forest), we run the same process with more trees running parallel. This is quite similar to the process of tree boosting with the difference being in how we train the models. More details on this can be found in the XGBoost documentation. From reading different views and research, XGBoost appears to be faster to train than gradient boosting and even random forest and generally delivers better results.

from xgboost import XGBClassifiery = dat['Class']X = dat.drop(['Class'],axis=1)X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=100)xgb = XGBClassifier()#fine tuning XGB parametersparams = {'min_child_weight':[5,15],          'subsample':[0.6,0.8,1.0],          'gamma':[1,5,10,15],          'learning_rate': [0.01,0.05,0.1],          'colsample_bytree':[0.6,0.8,1.0],          'max_depth':[2,3,5,10],          'n-estimaors': range(50,1000,50)    }#randomized searchrandom_search = RandomizedSearchCV(xgb,params,cv=5,n_iter=5,scoring='f1',random_state=100)random_search.fit(X_train,y_train)confusion_matrix(y_test,opt_predicts)

#### RESULTS ####

array([[85290,    11],       [   31,   111]])

Once again, I decided to find the optimal parameters using randomised search after reading about benchmark gamma, and learning rates and fitted the model to my training data, getting a slight improvement in my model. My model now correctly classifies normal transactions with 99.987% accuracy and 78.16% accuracy for fraudulent transactions.

print(classification_report(y_test,opt_predicts))

#### RESULTS ####

             precision    recall  f1-score   support           0       1.00      1.00      1.00     85301           1       0.91      0.78      0.84       142   micro avg       1.00      1.00      1.00     85443   macro avg       0.95      0.89      0.92     85443weighted avg       1.00      1.00      1.00     85443

More exciting is the slight increase in the average f1 macro average score. The most interesting lesson from this exercise was that the biggest jumps in performance did not come from using different models, they instead came from feature engineering. This would presumably be even more feasible when dealing with data that you have a deeper contextual understanding of. If for example, you are a payments platform you would probably have a deeper understanding of the average size, volume and transaction times for a given user and could potentially create aggregated features to better learn from patterns that are not explicit in raw data.

Small improvement, but improvement none the lessCross-Validation

As the final step, I needed to cross validate my XGBoost results. In one of my previous blogs, I gave a high-level description of k-fold validation. For this project, I specifically opted to use 10 fold stratified cross-validation. The idea behind this is to ensure that each fold is a good representation of the entire dataset and doesn’t for example only contain data from class 0 (normal transactions). This is especially important in this scenario since a little over 99% of transactions are one class.

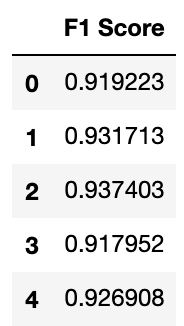
strat = StratifiedKFold(n_splits=5, shuffle=True)strat.get_n_splits(X)model_score = []for train_index, test_index in strat.split(X,y):    X_train,X_test,y_train,y_test = X.iloc[train_index], X.iloc[test_index],y.iloc[train_index],y.iloc[test_index]    random_search.fit(X_train, y_train)    xgb_predicts=random_search.predict(X_test)    model_score.append(f1_score(y_test,xgb_predicts,average='macro',labels=np.unique(xgb_predicts)))scores_table = pd.DataFrame({"F1 Score" :model_score})scores_table

With the cross-validation, I am specifically looking to validate the macro f1 score- which according to my initial test was about 0.92.

Results

I then appended the 5 tests to a dataframe. The results kind of validate the initial results I had.

Fraud detection is a topic I am quite interested and will be doing a bit more work on this model on my Github and Kaggle account.

Thus concludes my analysis.

Feel free to reach out with any comments, questions, criticisms, banter, reading suggestions or freebies (really doesn’t matter what it is — I like free things) on my Twitter.

Detecting Fraudulent Transactions was originally published in Hacker Noon on Medium, where people are continuing the conversation by highlighting and responding to this story.